恒定函数做市商

本章重述了Uniswap V2的白皮书。理解这些数学原理对构建类似Uniswap的DEX至关重要，但如果你现在不能完全理解也不用担心。

正如我在上一节中提到的，构建AMM有不同的方法。我们将专注构建一种特定类型的AMM——恒定函数做市商。不要被这个长名字吓到！其核心是一个非常简单的数学公式：

$$x\ast y=k$$

就是这样，这就是AMM。

$x$和$y$是pool合约的储备金——它当前持有的代币数量。k是它们的乘积，实际值并不重要。

为什么只有两个储备金额，x和y？
每个Uniswap pool只能持有两种代币。我们使用x和y来指代一个pool的储备，其中x是第一种代币的数量，y是另一种代币的数量，顺序并不重要。

恒定函数公式表明：每次交易后，k必须保持不变。当交易者进行交易时，他们将一定数量的一种代币放入pool中（他们想要出售的代币），并从pool中取出一定数量的另一种代币（他们想要购买的代币）。这改变了pool的储备，而恒定函数公式要求储备的乘积不能改变。正如我们将在本书中多次看到的，这个简单的要求是Uniswap工作原理的核心算法。

交易函数

现在我们知道了什么是流动性池，让我们写出pool中交易发生的公式：

$$(x+r\Delta x)(y-\Delta y)=k$$

1. 有一个流动性池，其中包含一定数量的代币0（$x$）和一定数量的代币1（$y$）
2. 当我们用代币0购买代币1时，我们向pool中提供一定数量的代币0（$\Delta x$）。
3. pool给我们一定数量的代币1作为交换（$\Delta y$）。
4. pool还从我们提供的代币0数量中收取一小部分费用（$r=1-\text{交换费用}$）。
5. 代币0的储备发生变化（$x+r\Delta x$），代币1的储备也发生变化（$y-\Delta y$）。
6. 更新后的储备的乘积仍然必须等于$k$。

我们将使用代币0和代币1的表示法来表示这些代币，因为这是它们在代码中的引用方式。在这一点上，哪个是0哪个是1并不重要。

我们基本上是给pool一定数量的代币0，并获得一定数量的代币1。pool的工作是以公平的价格计算并给我们正确数量的代币1。这让我们得出以下结论：pool决定交易价格。

定价

我们如何计算pool中代币的价格？

由于Uniswap pool是独立的智能合约，pool中的代币是相对于彼此定价的。例如：在ETH/USDC pool中，ETH是以USDC定价的，USDC是以ETH定价的。如果1 ETH价值1000 USDC，那么1 USDC价值0.001 ETH。对于任何其他pool来说都是如此，无论是稳定币对还是非稳定币对（例如ETH/BTC）。

在现实世界中，一切都是基于供需法则定价的。这对AMM也同样适用。我们暂时把需求部分放在一边，专注于供给。

pool中代币的价格由代币的供给决定，也就是由pool持有的代币储备量决定。代币价格简单地是储备的比率：

$$P_x=\frac{y}{x}，P_y=\frac{x}{y}$$

其中$P_x$和$P_y$是以另一种代币为单位的代币价格。

这样的价格被称为现货价格，它们只反映当前的市场价格。然而，实际交易的价格是以不同方式计算的。这就是我们需要把需求部分带回来的地方。

从供需法则得出的结论是，高需求会增加价格——这是我们在无许可系统中需要的一个属性。我们希望当需求高时价格也高，我们可以使用pool储备来衡量需求：你想从pool中移除的代币越多（相对于pool的储备），需求的影响就越大。

让我们回到交易公式，仔细看看：

$$(x+r\Delta x)(y-\Delta y)=xy$$

如你所见，我们可以从中推导出${\Delta }_x$和$\Delta y$，这意味着我们可以根据输入金额计算交易的输出金额，反之亦然：

$$\Delta y=\frac{yr\Delta x}{x+r\Delta x}$$ $$\Delta x=\frac{x\Delta y}{r(y-\Delta y)}$$

事实上，这些公式使我们不必计算价格！我们总是可以使用$\Delta y$公式找到输出金额（当我们想卖出已知数量的代币时），我们总是可以使用$\Delta x$公式找到输入金额（当我们想买入已知数量的代币时）。注意，这些公式中的每一个都是储备的关系（$x/y$或$y/x$），它们还考虑了交易金额（前者中的$\Delta x$和后者中的$\Delta y$）。这些是同时考虑供给和需求的定价函数。而我们甚至不需要计算价格！

以下是如何从交易函数推导出上述公式： $$(x+r\Delta x)(y-\Delta y)=xy$$ $$y-\Delta y=\frac{xy}{x+r\Delta x}$$ $$-\Delta y=\frac{xy}{x+r\Delta x}-y$$ $$-\Delta y=\frac{xy-y(x+r\Delta x)}{x+r\Delta x}$$ $$-\Delta y=\frac{xy-xy-yr\Delta x}{x+r\Delta x}$$ $$-\Delta y=\frac{-yr\Delta x}{x+r\Delta x}$$ $$\Delta y=\frac{yr\Delta x}{x+r\Delta x}$$ 以及： $$(x+r\Delta x)(y-\Delta y)=xy$$ $$x+r\Delta x=\frac{xy}{y-\Delta y}$$ $$r\Delta x=\frac{xy}{y-\Delta y}-x$$ $$r\Delta x=\frac{xy-x(y-\Delta y)}{y-\Delta y}$$ $$r\Delta x=\frac{xy-xy+x\Delta y}{y-\Delta y}$$ $$r\Delta x=\frac{x\Delta y}{y-\Delta y}$$ $$\Delta x=\frac{x\Delta y}{r(y-\Delta y)}$$

曲线

上述计算可能看起来过于抽象和枯燥。让我们将恒定乘积函数可视化，以更好地理解它是如何工作的。

当绘制时，恒定乘积函数是一个二次双曲线：

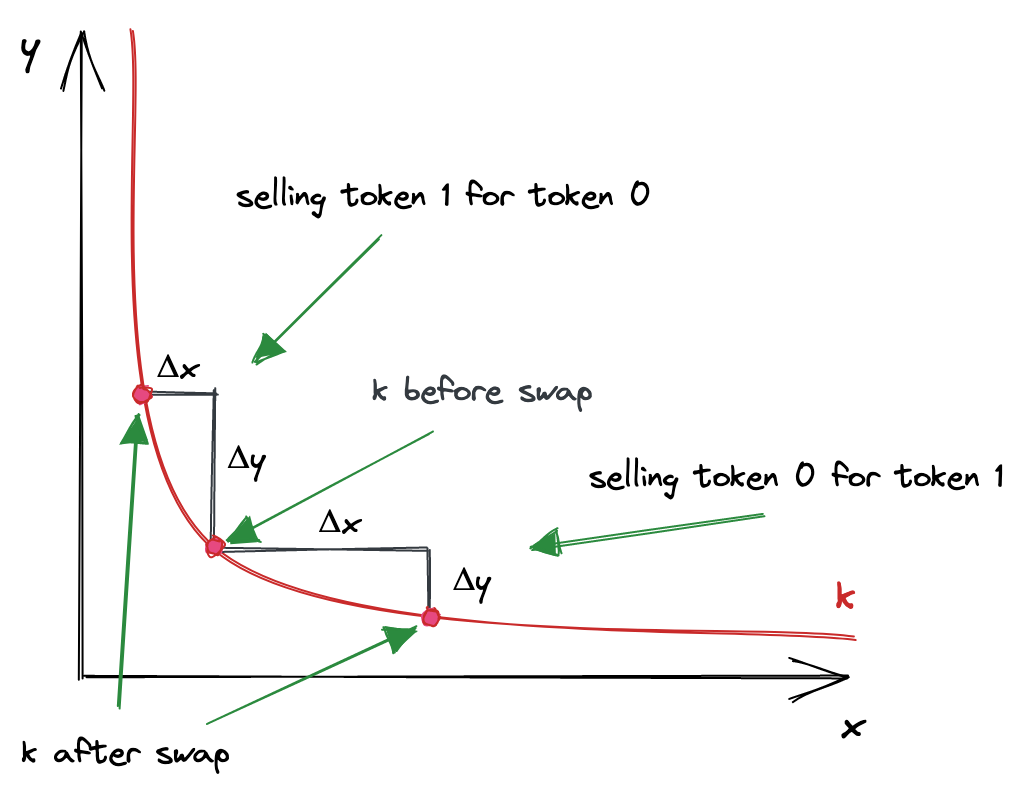
其中轴是pool储备。每次交易都从曲线上对应于当前储备比率的点开始。为了计算输出金额，我们需要在曲线上找到一个新点，该点的$x$坐标为$x+\Delta x$，即代币0的当前储备+我们正在出售的金额。$y$的变化就是我们将获得的代币1的数量。

让我们看一个具体的例子：

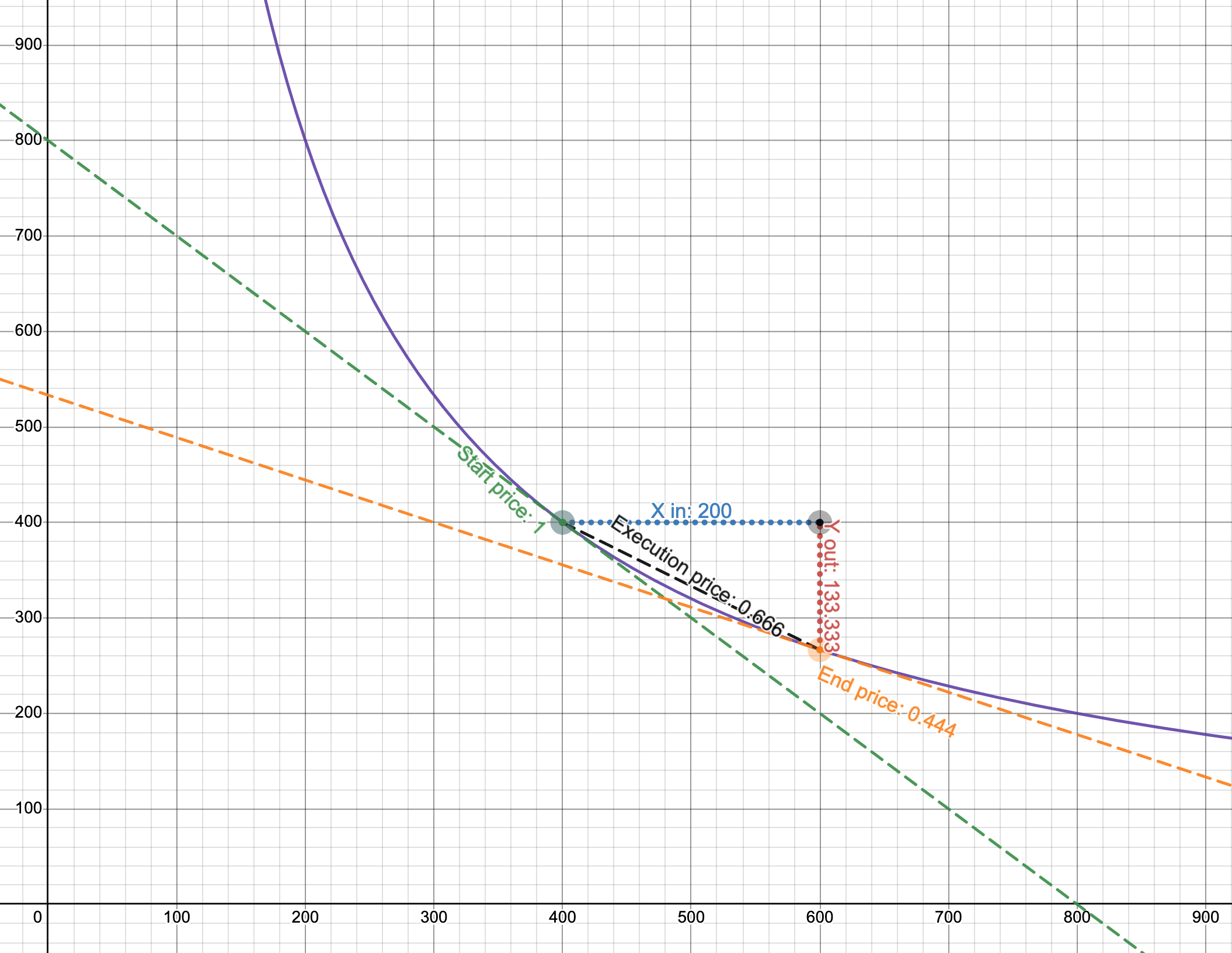
1. 紫色线是曲线，轴是pool的储备（注意它们在起始价格时是相等的）。
2. 起始价格是1。
3. 我们正在出售200个代币0。如果我们只使用起始价格，我们期望得到200个代币1。
4. 然而，执行价格是0.666，所以我们只得到133.333个代币1！

这个例子来自Desmos图表，由Uniswap的创造者之一Dan Robinson制作。为了更好地理解它是如何工作的，试着设想不同的场景并在图表上绘制它们。尝试不同的储备，看看当$\Delta x$相对于$x$很小时输出金额如何变化。

据传说，Uniswap是在Desmos中发明的。

我打赌你在想为什么要使用这样的曲线。它看起来像是在惩罚你进行大额交易。这是真的，而且这是一个理想的属性！供需法则告诉我们，当需求高（而供给恒定）时，价格也高。当需求低时，价格也较低。这就是市场的运作方式。而神奇的是，恒定乘积函数实现了这种机制！需求由你想要购买的数量定义，供给是pool储备。当你想要购买的数量相对于pool储备较大时，价格比你想要购买较小数量时更高。这么简单的公式保证了如此强大的机制！

尽管Uniswap不计算交易价格，我们仍然可以在曲线上看到它们。令人惊讶的是，在进行交易时有多个价格：

1. 交易前，有一个现货价格。它等于储备的比率，$\frac{y}{x}$或$\frac{x}{y}$，取决于交易的方向。这个价格也是起始点切线的斜率。
2. 交易后，在曲线上的另外一个点上有一个新的现货价格。它是这个新点切线的斜率。
3. 交易的实际价格是连接这两点的线的斜率！

这就是Uniswap的全部数学！呼！

好吧，这是Uniswap V2的数学，而我们正在研究Uniswap V3。所以在下一部分，我们将看到Uniswap V3的数学有何不同。